 pour 10 (d'après
pour 10 (d'après
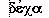 , H pour 100 (d'après
, H pour 100 (d'après 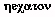 où le
où le
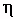 note en fait l'esprit rude de ce qui, en graphie plus moderne,
deviendra
note en fait l'esprit rude de ce qui, en graphie plus moderne,
deviendra 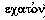 ) etc...
) etc...
Le système de numération dont nous usons fait appel à la base 10. Utilisée par les Egyptiens, cette base fut aussi employée par les Indiens, les Sémites Occidentaux et les Grecs. Dans la mesure où 10 correspond au nombre total des doigts des deux mains, cette base nous paraît la plus naturelle. Ce n'est pourtant nullement la seule possible.
En Amérique précolombienne, par exemple, les Mayas et les Aztèques avaient recours à la base 20. En France même, on connaît un exemple d'utilisation de cette base puisqu'on dit " quatre-vingt " pour 80. A priori, une telle base peut sembler aussi naturelle que la base 10 dans la mesure où 20 est aussi un nombre total de doigts: ceux des deux mains plus ceux des deux pieds.
Désirant vraisemblablement combiner les propriétés de la base 6 et celles de la base 10, les Sumériens ont inventé un système de numération mixte faisant appel à la base 60 pour les ordres principaux (tels que 60, 3600 et 216000) et à la base 10 pour des ordres intercalaires (10, 600 = 10 * 60, 36000 = 10 * 3600 etc...). Ce système complexe nous a d'ailleurs été partiellement transmis puisque c'est de là que nous viennent les 60 secondes de nos 60 minutes ainsi que les 360° de nos angles.
Pour traduire un système de numération sous forme scripturale, il a fallu élaborer un certain nombre de techniques.
La plus ancienne, sans doute, a consisté en le fait d'écrire les nombres comme on écrivait les autres mots: sous une forme phonétique ou d'idéogramme. Jusqu'au VIIIe siècle avant notre ère, ni les Phéniciens, ni les Araméens ne semblent avoir eu recours aux chiffres et, même, bien après leur introduction, il est demeuré courant de juxtaposer, comme on le fait d'ailleurs aujourd'hui sur les chèques, la notation en chiffres et la notation en toutes lettres.
Cependant, comme le fait d'écrire les nombres comme des
mots ordinaires ne pouvait manquer d'être pesant, d'autres
techniques de notation ont été expérimentées.
On s'est, par exemple, mis à noter les ordres de la base
de numérotation par l'initiale des mots désignant
les nombres correspondants. C'est ainsi que dans le système
dit " hérodien " et employé par certains
Grecs, on notait ainsi  pour 10 (d'après
pour 10 (d'après
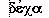 , H pour 100 (d'après
, H pour 100 (d'après 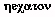 où le
où le
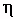 note en fait l'esprit rude de ce qui, en graphie plus moderne,
deviendra
note en fait l'esprit rude de ce qui, en graphie plus moderne,
deviendra 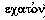 ) etc...
) etc...
Un autre procédé a consisté à recourir aux lettres d'un alphabet en leur affectant une valeur numérique suivant leur position dans les abécédaires. Ainsi, pour numéroter les livres de l'Iliade et de l'Odyssée, on a fait appel aux lettres de l'alphabet Grec auxquelles on donnait pour valeur 1 à 24 suivant leur position. Par ailleurs, et afin de pouvoir noter aussi des nombres plus élevés, les Grecs ont élaboré un autre système de numérotation qui, s'il faisait aussi appel aux lettres de leur alphabet, leur adjoignait des signes.
Une autre technique a été d'introduire des caractères spécialisés pour noter les nombres (les chiffres) distincts des caractères normaux de l'écriture. Les Mayas ont noté 1 par le point, 5 par un trait. Les Egyptiens ont notés 1 par l'encoche, 10 par l'anse et 100 par la corde enroulée.
Tout ceci a permis de rendre possible la numération par juxtaposition: un nombre doit ainsi être lu comme la somme des chiffres qui le composent. Ainsi, chez les Egyptiens 467 est noté 4*100 + 6*10 + 7*1. Dans ce système, on dispose d'un signe par ordre de la base et on le répète autant de fois que nécessaire (de 0 à 9 fois en base 10 par exemple).
Les Romains possédaient également un système de numération par juxtaposition, mais il était compliqué par le fait que, pour la lecture d'un nombre, certains chiffres devaient être retranchés les uns aux autres au lieu d'être ajoutés (4 était noté IV c'est à dire 5 - 1 et non IIII c'est à dire 1 + 1 + 1 + 1). Les Romains faisaient appel aux 7 signes de numérations suivants: I. V. X. L. C. D. M. (1, 5, 10, 50, 100, 500 et 1000). Le V n'est que la moitié supérieure de X. Quant aux autres signes, ils dérivent des trois consonnes Grecques inutilisées par la langue latine: le psi s'est affaissé à droite pour donner L; le theta s'est ouvert en C et le phi qui valait 1000 (devenu M au Ier siècle) a donné, par sa moitié droite D (500). Ces chiffres Romains furent utilisés en Europe durant tout le Moyen-Age.
Afin de mettre au point un système permettant de limiter le nombre de chiffre tout en rendant possible la notation de tout nombre, aussi élevé soit-il, il restait à introduire la numérotation de position.
Dès le Moyen-Empire, les Egyptiens furent sur la voie de ce système. Ils renoncèrent tout d'abord à utiliser les chiffres les plus élevés (tels que 100000 ou 1000000) et entreprirent de noter les nombres élevés par une méthode de position faisant appel aux chiffres des ordres inférieurs (c'est à dire 1, 10 et 100) qu'on plaçait au dessous des chiffres d'ordre plus élevé. C'est ainsi qu'on a noté 40000 comme 4 * 10000) et non comme 10000 + 10000 + 10000 + 10000.
Victorieux des Sumériens, les Assyro-babyloniens cessèrent d'utiliser la base 60 pour l'usage courant. Ils conservèrent cependant l'ancien système en Mathématique et en Astronomie: c'est ainsi que 75 doit se lire 1 degré 15 minutes et non 60 + 15. Dans un tel système c'est la position relative des chiffres qui donne leur grandeur (s'agit-il de degrés, de minutes ou de secondes?). Dans la mesure cependant où un ordre peut manquer, il faut l'indiquer: c'est ainsi que, pour la première fois dans l'Histoire, on introduit le zéro, attesté en Babylonie au moins depuis la période hellénistique (1 degré 15 secondes va ainsi se noter 1 degré 0 minute et 15 secondes).
C'est aux Indiens, cependant, que revient le mérite d'introduire, avec les chiffres nagari, un système analogue au nôtre, c'est à dire faisant appel à la base 10 et à une numérotation de position avec zéro.
Les chiffres nagari semblent avoir été empruntés
aux Indiens par les Arabes orientaux du IXe siècle (qui
ont appelé ces chiffres hindi du fait de cet emprunt) qui
les ont ensuite transmis aux Byzantins et aux Arabes Occidentaux
(qui ont appelé leurs chiffres gubari). Par la suite, au
Xe siècle, ces derniers ont permis l'introduction de ces
chiffres en Espagne et en Occident sous la dénomination
de chiffres Arabes. Les chiffres 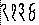 Indiens
devinrent
Indiens
devinrent 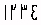 chez les Arabes et 1234 en Occident. Jusqu'au
XIIIe siècle, les chiffres Arabes restèrent cependant
d'un usage très restreint en Europe. Le mérite de
leur diffusion revient surtout au mathématicien pisan Leonardo
Fibonacci, auteur d'un Liber abaci en 1202.
chez les Arabes et 1234 en Occident. Jusqu'au
XIIIe siècle, les chiffres Arabes restèrent cependant
d'un usage très restreint en Europe. Le mérite de
leur diffusion revient surtout au mathématicien pisan Leonardo
Fibonacci, auteur d'un Liber abaci en 1202.
L'usage du zéro n'apparut en Occident qu'au XIIe siècle, après la traduction de traités de mathématiques Arabes, en particulier celui du célèbre Al-Kharizmi. Le nom Arabe du zéro, sifr (vide) provient de la racine safira (être vide). Il a donné zefiro en italien, puis zéro ainsi que chiffre en français. Une étymologie contestée suppose qu'au départ, sifr n'aurait pas voulu dire vide (chez les Indiens pourtant un même mot, çunya, désigne à la fois vide et zéro) mais viendrait du mot sipos, lui-même une déformation du Grec psephos (caillou, jeton). Le sipos aurait été un jeton sans marque employé dans certains cas mal définis pour des calculs sur abaques.